“Math is hard” — if you are an LLM – and why that matters
No matter how much data you train them on, they still don’t truly understand multiplication.
Some Reply Guy on X assured me yesteday that “transformers can multiply”. Even pointed me to a paper, allegedly offering proof.
The paper turns out to be pretty great, doing exactly the right test, but it doesn’t prove what its title alleges. More like the opposite.
The paper alleges “GPT Can Solve Mathematical Problems Without a Calculator.” But it doesn’t really show that, except in the sense that I can shoot free throws in the NBA, Sure, I can toss the ball in the air, and sometimes I might even sink a shot, the more so with practice; but I am probably going to miss a lot, too. And 70% would be great for free throws; for multiplication it sucks. 47323 * 19223 = 909690029 and it shall always be; no partial credit for coming close.
Here’s what actually happened, in the paper in question: The authors trained their 2 billion parameter model, called MathGLM, on an enormous, 50 million record custom “ dataset .. designed to encompass a wide spectrum of arithmetic operations, spanning from straightforward 1-atomic operation to more complex 9-atomic operations.” The authors add that : By adopting this step-by-step strategy, MathGLM learns to handle both simple and intricate arithmetic expressions, which empowers it to accurately perform calculations even for operations involving multiplication of numbers greater than 8 digits, and those with decimals and fractions. Moreover, we incorporate the concept of curriculum learning to further augment the capabilities of MathGLM.” My (innately-programmed) calculator by contrast has received no training at all.
Let’s compare, and start easy: 5 digit multiplication problems.
The 2B model does better (85.16%) as expected than a smaller version, trained on MathGLM-500m (83.45), MathGLM-500, and crushes both ChatGPT (5.43%) and GPT (6.64%). Very impressive, relatively speaking. But then again any pocket calculator would score 100%. So there’s still obviously room for improvement.
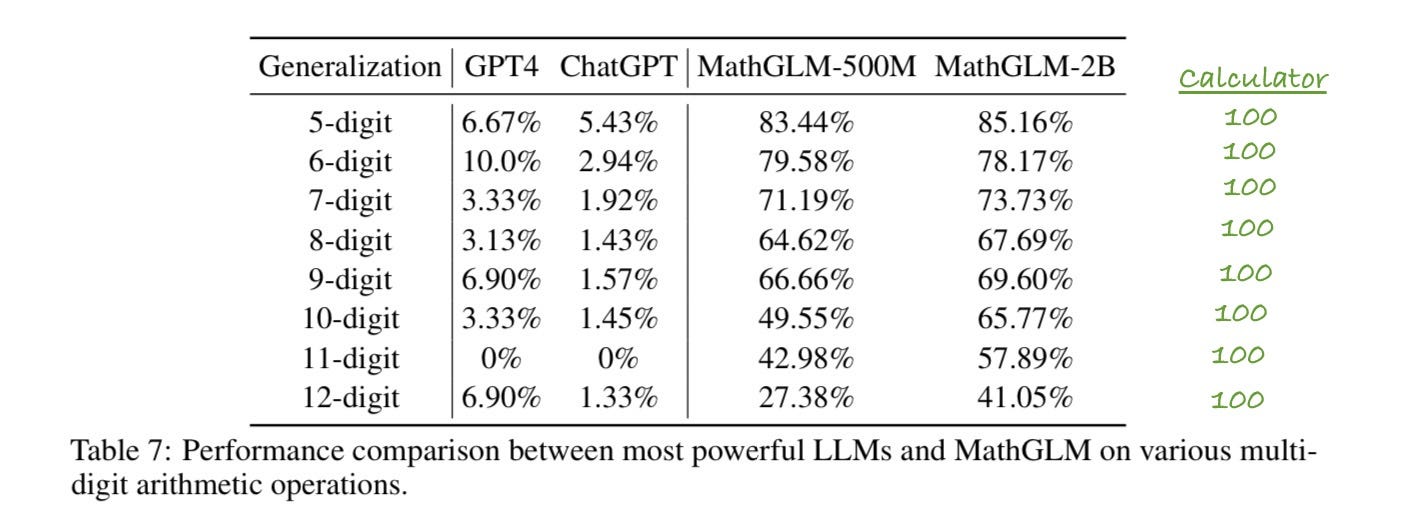
What happens if we try bigger and bigger math problems, in which the training space is less densely covered? Fortunately, the authors tested exactly that, reporting results in their Table 7. The biggest, best model is MathGLM-2B; as a baseline that should have been included in the paper,I have taken the liberty of adding the expected results from a calculator on the right, in green.
Notice anything? It’s not just that the performance on MathGLM steadily declines as the problems gets bigger, with the discrepancy between it and a calculator steadily increasing, it’s that the LLM based system is generalizing by similarity, doing better on cases that are in or near the training set, never, ever getting to a complete, abstract, reliable representation of what multiplication is. A calculator, without the benefit of 2B parameters, would be at 100%, because it is programmed, at the factory, with an algorithm that actually computes multiplication. The LLM never induces such an algorithm. That, in a nutshell, is why we should never trust pure LLMs; even under carefully controlled circumstances with massive amounts of directly relevant data, they still never really get even the most basic linear functions. (In a recent series of posts on X, Daniel Litt has documented a wide variety of other math errors as well.) Some kind of hybrid may well work, but LLMs on their own remain stuck.
§
As a brief postscript, Steven Pinker and I were making nearly identical arguments about English past tense verbs in the early 1990s, suggesting that children learned some aspects of language (eg irregular verbs) in similarity-driven ways, but others (e.g. regular verbs) in a more abstract, similarity-independent way that was out of reach of the precursors to deep learning that were then popular. Thirty years later, the same Achilles’ Heel remains.
Gary Marcus feels really old whenever he has to write articles like this. He had really hoped to have said his last word about them in 2001, when he wrote The Algebraic Mind. When the field finally figures out how to learn algebraic abstractions from data, reliably, his work will finally be done.



My 1976 vintage ELF has a dedicated math ROM alongside its interpreter. Later PCs used math co-processors. I don't understand why LLM devotees seem to shun hybrid processing solutions as sacrilegeous...
There are two kinds of AI researcher: (1) those who already know that LLMs (by themselves) are not the route to human-level AGI, and (2) those who need to spend 10-20 years and $100 billion working that out.